Millions of americans suffer from one form or another of arthritis
Cats on Cal Newsletter, Volume 9, December 2007 256 U.S. Route One, Scarborough ME 04074 – (207) 883-7000 Inflammatory Bowel Disease: Simplifying a Complex Disease Do you frequently* come home to find vomit on your The first step is to perform fresh fecal exams to dining room rug? Does your feline companion check for parasitic and bacterial agents. The next occasionally defecate outsid
 CHARMM FORCE FIELD PARAMETERIZATION OF ROSIGLITAZONE
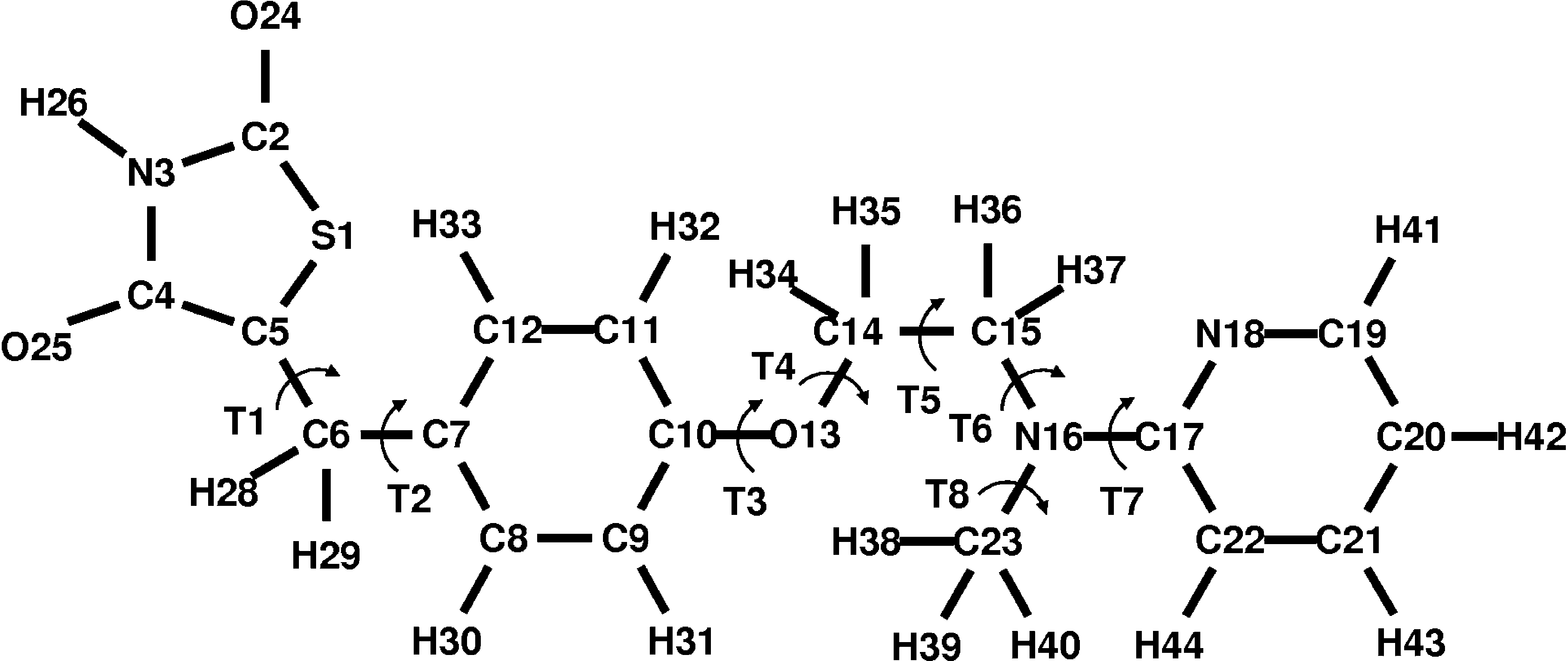
FIGURE 1. Chemical structure of rosiglitazone. The arc-shaped arrows indicate the torsion (T) of the eight bonds forwhich full revolution is possible.
CHARMM FORCE FIELD PARAMETERIZATION OF ROSIGLITAZONE
FIGURE 1. Chemical structure of rosiglitazone. The arc-shaped arrows indicate the torsion (T) of the eight bonds forwhich full revolution is possible.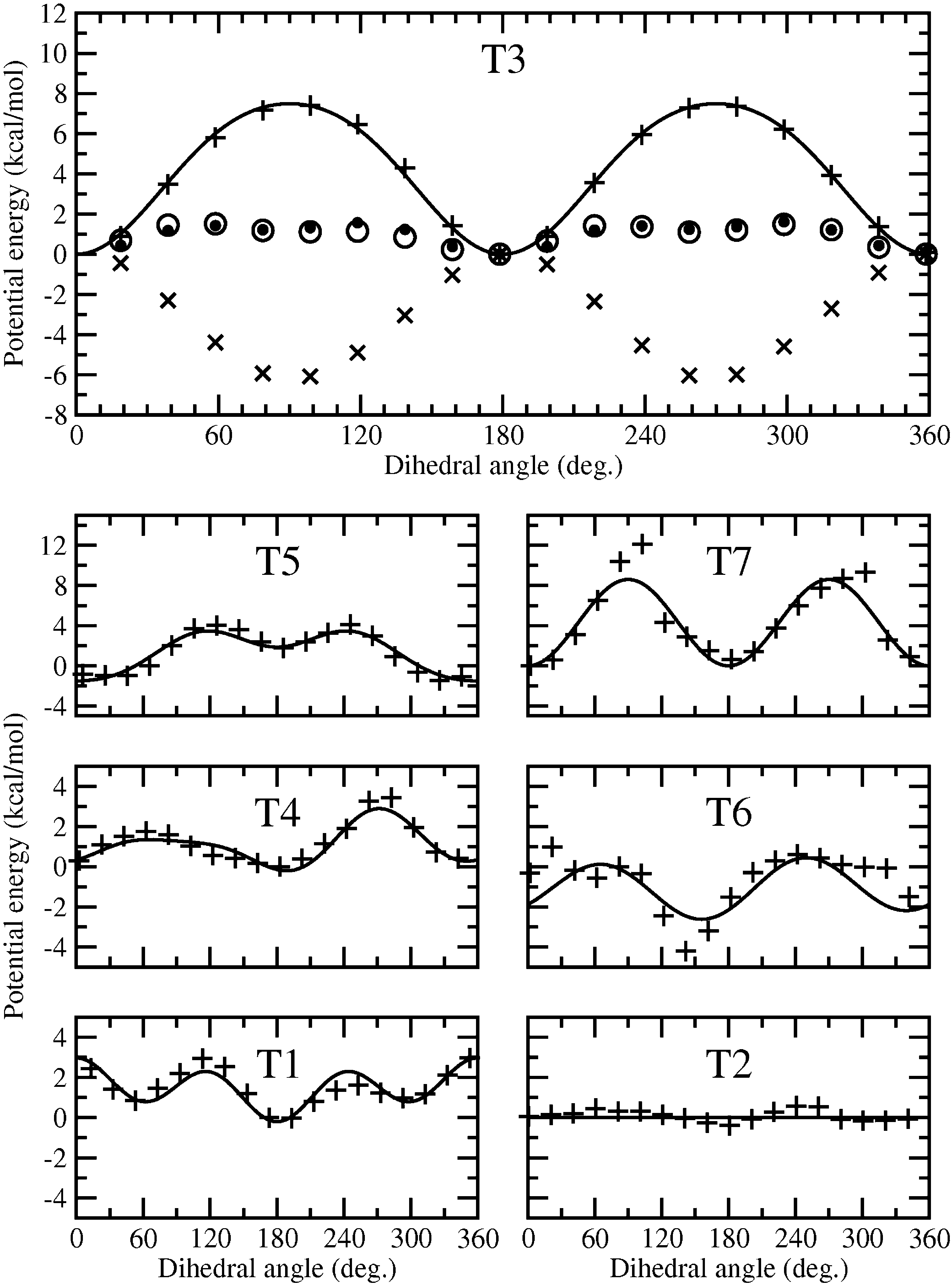 CHARMM FORCE FIELD PARAMETERIZATION OF ROSIGLITAZONE
FIGURE 2. Torsion energies of the bonds C5-C6 (T1), C6-C7 (T2), C10-O13 (T3), O13-C14 (T4), C14-C15 (T5), C15-N16 (T6), and N16-C17 (T7). The black dots represent the ab initio PES, whereas the crosses (x) indicate the forcefield PES without the considered dihedral angle. The difference between them is shown by plus signs (þ) and theadjusted potential energy of the dihedral angle is depicted by a solid line. For comparison, the circles show the totalforce field, including the parameterized dihedral angle.
CHARMM FORCE FIELD PARAMETERIZATION OF ROSIGLITAZONE
FIGURE 2. Torsion energies of the bonds C5-C6 (T1), C6-C7 (T2), C10-O13 (T3), O13-C14 (T4), C14-C15 (T5), C15-N16 (T6), and N16-C17 (T7). The black dots represent the ab initio PES, whereas the crosses (x) indicate the forcefield PES without the considered dihedral angle. The difference between them is shown by plus signs (þ) and theadjusted potential energy of the dihedral angle is depicted by a solid line. For comparison, the circles show the totalforce field, including the parameterized dihedral angle.
 TABLE IIDihedral parameters for seven torsional rotations.
TABLE IIDihedral parameters for seven torsional rotations.